 |
Download the current version of the Recursive Zonal Equal Area (EQ) Sphere Partitioning Toolbox from the EQ Sphere Partitions project page hosted at SourceForge.
The Recursive Zonal Equal Area (EQ) Sphere Partitioning Toolbox is a suite of Matlab functions. These functions are intended for use in exploring different aspects of EQ sphere partitioning.
The functions are grouped into the following groups of tasks:
An EQ partition is a partition of S^dim [the unit sphere in the dim+1 Euclidean space R^(dim+1)] into a finite number of regions of equal area. The area of each region is defined using the Lebesgue measure inherited from R^(dim+1).
The diameter of a region is the sup of the Euclidean distance between any two points of the region. The regions of an EQ partition have been proven to have small diameter, in the sense that there exists a constant C(dim) such that the maximum diameter of the regions of an N region EQ partition of S^dim is bounded above by C(dim)*N^(-1/dim).
An EQ point set is the set of center points of the regions of an EQ partition. Each region is defined as a product of intervals in spherical polar coordinates. The center point of a region is defined via the center points of each interval, with the exception of spherical caps and their descendants, where the center point is defined using the center of the spherical cap.
For details of changes from earlier versions of the EQ partitioning code, and changes from 1.00 to the current release, see CHANGELOG.
This toolbox has been tested with various Matlab versions between R2020b and R2023b on Linux, MacOS and Windows 10.
This toolbox is organized into a number of directories. To use it effectively, these directories need to be on your Matlab path every time you start Matlab. You will therefore need to install the toolbox before using it.
To do this,
The user documentation includes the help comments in each Matlab M file, plus the extra files Contents.m, AUTHORS, CHANGELOG, COPYING, INSTALL.txt and README.txt.
The extra files contain the following:
To see a brief description of the functions in the toolbox, enter the command HELP EQ_SPHERE_PARTITIONS (in lower case). The command WHAT lists all the functions in your current directory.
For each function, the command HELP FUNCTION, where FUNCTION is the name of the function, will give the help for the function.
The help format is:
For example, here is the result of HELP EQ_POINT_SET:
EQ_POINT_SET Center points of regions of EQ partition, in Cartesian coordinates
Syntax
points_x = eq_point_set(dim,N,options);
Description
POINTS_X = EQ_POINT_SET(dim,N) does the following:
1) uses the recursive zonal equal area sphere partitioning algorithm to
partition S^dim (the unit sphere in dim+1 dimensional space) into N regions
of equal area and small diameter, and
2) sets POINTS_X to be an array of size (dim+1 by N), containing the center
points of each region.
Each column of POINTS_X represents a point of S^dim, in Cartesian coordinates.
The arguments dim and N must be positive integers.
POINTS_X = EQ_POINT_SET(dim,N,'offset','extra') uses experimental extra offsets
for S^2 and S^3 to try to minimize energy.
POINTS_X = EQ_POINT_SET(dim,N,extra_offset) uses experimental extra offsets if
extra_offset is true or non-zero.
Notes
Each region is defined as a product of intervals in spherical polar
coordinates. The center point of a region is defined via the center points
of each interval, with the exception of spherical caps and their descendants,
where the center point is defined using the center of the spherical cap.
If dim > 3, extra offsets are not used.
For more details on options, see help partition_options.
Examples
>> points_x = eq_point_set(2,4)
points_x =
0 0.0000 -0.0000 0.0000
0 1.0000 -1.0000 0
1.0000 0.0000 0.0000 -1.0000
>> size(points_x)
ans =
3 4
See also
PARTITION_OPTIONS, EQ_POINT_SET_POLAR, EQ_REGIONS, POLAR2CART
The help for each function briefly describes the input and the output, as per the example for eq_point_set above.
You need to find a function which does what you want to do. Examples:
points_x = eq_point_set(dim,N);
points_s = (eq_point_set_polar(dim,N);
regions = eq_regions(dim,N);
diam_bound = eq_diam_bound(dim,N);
[energy,dist] = eq_energy_dist(dim,N,s);
count_v = eq_count_points_by_s2_region(points_s, 8);
project_s2_partition(N);
In principle, any function which has dim as a parameter will work for any integer dim >= 1. In practice, for large d, the function may be slow, or may consume large amounts of memory.
In principle, any function which takes N as an argument will work with any positive integer value of N. In practice, for very large N, the function may be slow, or may consume large amounts of memory.
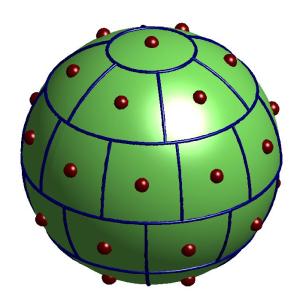
A number of different illustrations are available:
show_s2_partition(N);
project_s2_partition(N);
project_s3_partition(N);
illustrate_eq_algorithm(dim,N);
See the help for these functions for details.
Toolbox Installer 2.2, 2003-07-22 by Rasmus Anthin.
Files modified and relicenced with permission of Rasmus Anthin:
./private: install.m uninstall.m
| |